Cross Product Two Dimensions

Answer 1 of 5. 1 After performing the cross.

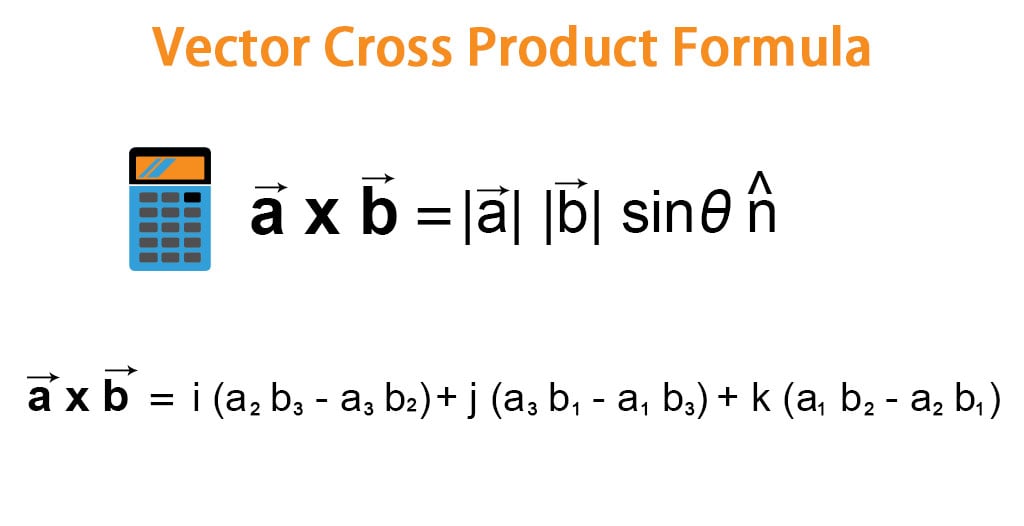
Vector Cross Product Formula Examples With Excel Template

Length of two vectors to form a cross product.

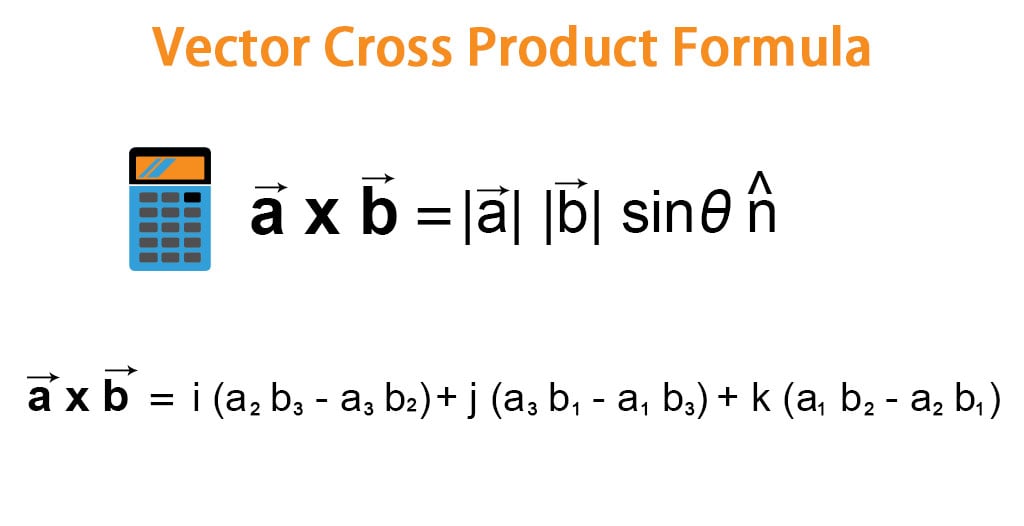
. In this final section of this chapter we will look at the cross product of two vectors. However if you choose a three-dimensional subspace of R 4 then that subspace inherits the inner product which uniquely determines a cross product up to choice of orientation. The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a b.

In higher dimensions the orthogonal complement of a k plane is an n-k plane so the cross product of two vectors would be an n-2 dimensional object. The cross product has only been defined for three dimensions. The cross product a b is defined as a vector c that is perpendicular orthogonal to both a and b.

This means that you dont get a true cross-product in two dimensional space. Lubošs answer is correct and efficient but for someone new to vector. In mathematics the cross product or also known as the vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol X.

We should note that the cross product requires both of the. The 1st parameter is a the. In three-dimensional space the cross product is a binary operation on two vectors.

The method returns c the Vector cross product s. It generates a perpendicular vector to both the given vectors. From the definition of the cross product we find that the cross product of two parallel or collinear vectors is zero as the sine of the angle between them 0 or 1 8 0 is zeroNote that.

In physics and applied mathematics the wedge notation a b is often used in conjunction with the name vector product although in pure mathematics such notation is usually reserved for just the exterior product an abstraction of the vector product to n dimensions. To compute the cross product of two vectors use the numpycross method in Python Numpy. It is simpler to just.

Vector Product of 2 vectors a i b j c k and A i B j C k is given by the determinant i j k a b c A B C. Section 5-4. Cross Product of Two Vectors.

I find its possible to define a. The cross product is a mathematical operation which can be done between two three-dimensional vectors. The properties of a cross product can vary depending on the type of cross-product formula that is used.

It is often represented by the symbol. General Properties of a Cross Product.

3 Ways To Calculate The Cross Product Of Two Vectors Wikihow

Cross Product Calculator Of Vectors

Cross Product Of Two Vectors Explained Youtube

Torque As A Vector Quantity